Turing Machines
A Turing Machine is an accepting device which accepts the languages
(recursively enumerable set) generated by type 0 grammars. It was
invented in 1936 by Alan Turing.
A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q0, B, F) where −
Here the transition 1Rq1 implies that the write symbol is 1, the tape moves right, and the next state is q1. Similarly, the transition 1Lq2 implies that the write symbol is 1, the tape moves left, and the next state is q2.
Time complexity all reasonable functions −
A TM accepts a language if it enters into a final state for any input
string w. A language is recursively enumerable (generated by Type-0
grammar) if it is accepted by a Turing machine.
A TM decides a language if it accepts it and enters into a rejecting state for any input not in the language. A language is recursive if it is decided by a Turing machine.
There may be some cases where a TM does not stop. Such TM accepts the language, but it does not decide it.
Solution
The Turing machine M can be constructed by the following moves −
Solution
Let us assume that the input string is terminated by a blank symbol, B, at each end of the string.
The Turing Machine, M, can be constructed by the following moves −
Multi-tape Turing Machines have multiple tapes where each tape is
accessed with a separate head. Each head can move independently of the
other heads. Initially the input is on tape 1 and others are blank. At
first, the first tape is occupied by the input and the other tapes are
kept blank. Next, the machine reads consecutive symbols under its heads
and the TM prints a symbol on each tape and moves its heads.
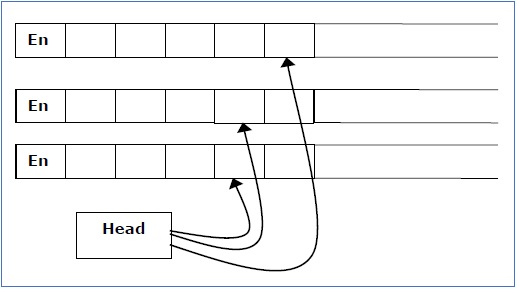 A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
Multi-track Turing machines, a specific type of Multi-tape Turing machine, contain multiple tracks but just one tape head reads and writes on all tracks. Here, a single tape head reads n symbols from n tracks at one step. It accepts recursively enumerable languages like a normal single-track single-tape Turing Machine accepts.
Multi-Track Turing Machine:
A Multi-track Turing machine can be formally described as a 6-tuple (Q, X, ∑, δ, q0, F) where −
Non-Deterministic Turing Machine:
In a Non-Deterministic Turing Machine, for every state and symbol, there are a group of actions the TM can have. So, here the transitions are not deterministic. The computation of a non-deterministic Turing Machine is a tree of configurations that can be reached from the start configuration.
An input is accepted if there is at least one node of the tree which is an accept configuration, otherwise it is not accepted. If all branches of the computational tree halt on all inputs, the non-deterministic Turing Machine is called a Decider and if for some input, all branches are rejected, the input is also rejected.
A non-deterministic Turing machine can be formally defined as a 6-tuple (Q, X, ∑, δ, q0, B, F) where −
The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.
It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.
Note − Turing machines with semi-infinite tape are equivalent to standard Turing machine
Definition
A Turing Machine (TM) is a mathematical model which consists of an infinite length tape divided into cells on which input is given. It consists of a head which reads the input tape. A state register stores the state of the Turing machine. After reading an input symbol, it is replaced with another symbol, its internal state is changed, and it moves from one cell to the right or left. If the TM reaches the final state, the input string is accepted, otherwise rejected.A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q0, B, F) where −
- Q is a finite set of states
- X is the tape alphabet
- ∑ is the input alphabet
- δ is a transition function; δ : Q × X → Q × X × {Left_shift, Right_shift}.
- q0 is the initial state
- B is the blank symbol
- F is the set of final states
Comparison with the previous automaton
The following table shows a comparison of how a Turing machine differs from Finite Automaton and Pushdown Automaton.| Machine | Stack Data Structure | Deterministic? |
|---|---|---|
| Finite Automaton | N.A | Yes |
| Pushdown Automaton | Last In First Out(LIFO) | No |
| Turing Machine | Infinite tape | Yes |
Example of Turing machine
Turing machine M = (Q, X, ∑, δ, q0, B, F) with- Q = {q0, q1, q2, qf}
- X = {a, b}
- ∑ = {1}
- q0 = {q0}
- B = blank symbol
- F = {qf }
| Tape alphabet symbol | Present State ‘q0’ | Present State ‘q1’ | Present State ‘q2’ |
|---|---|---|---|
| a | 1Rq1 | 1Lq0 | 1Lqf |
| b | 1Lq2 | 1Rq1 | 1Rqf |
Time and Space Complexity of a Turing Machine
For a Turing machine, the time complexity refers to the measure of the number of times the tape moves when the machine is initialized for some input symbols and the space complexity is the number of cells of the tape written.Time complexity all reasonable functions −
T(n) = O(n log n)
TM's space complexity −
S(n) = O(n)
A TM decides a language if it accepts it and enters into a rejecting state for any input not in the language. A language is recursive if it is decided by a Turing machine.
There may be some cases where a TM does not stop. Such TM accepts the language, but it does not decide it.
Designing a Turing Machine
The basic guidelines of designing a Turing machine have been explained below with the help of a couple of examples.Example 1
Design a TM to recognize all strings consisting of an odd number of α’s.Solution
The Turing machine M can be constructed by the following moves −
- Let q1 be the initial state.
- If M is in q1; on scanning α, it enters the state q2 and writes B (blank).
- If M is in q2; on scanning α, it enters the state q1 and writes B (blank).
- From the above moves, we can see that M enters the state q1 if it scans an even number of α’s, and it enters the state q2 if it scans an odd number of α’s. Hence q2 is the only accepting state.
M = {{q1, q2}, {1}, {1, B}, δ, q1, B, {q2}}
where δ is given by −| Tape alphabet symbol | Present State ‘q1’ | Present State ‘q2’ |
|---|---|---|
| α | BRq2 | BRq1 |
Example 2
Design a Turing Machine that reads a string representing a binary number and erases all leading 0’s in the string. However, if the string comprises of only 0’s, it keeps one 0.Solution
Let us assume that the input string is terminated by a blank symbol, B, at each end of the string.
The Turing Machine, M, can be constructed by the following moves −
- Let q0 be the initial state.
- If M is in q0, on reading 0, it moves right, enters the state q1 and erases 0. On reading 1, it enters the state q2 and moves right.
- If M is in q1, on reading 0, it moves right and erases 0, i.e., it replaces 0’s by B’s. On reaching the leftmost 1, it enters q2 and moves right. If it reaches B, i.e., the string comprises of only 0’s, it moves left and enters the state q3.
- If M is in q2, on reading either 0 or 1, it moves right. On reaching B, it moves left and enters the state q4. This validates that the string comprises only of 0’s and 1’s.
- If M is in q3, it replaces B by 0, moves left and reaches the final state qf.
- If M is in q4, on reading either 0 or 1, it moves left. On reaching the beginning of the string, i.e., when it reads B, it reaches the final state qf.
M = {{q0, q1, q2, q3, q4, qf}, {0,1, B}, {1, B}, δ, q0, B, {qf}}
where δ is given by −| Tape alphabet symbol | Present State ‘q0’ | Present State ‘q1’ | Present State ‘q2’ | Present State ‘q3’ | Present State ‘q4’ | |||
|---|---|---|---|---|---|---|---|---|
| 0 | BRq1 | BRq1 | ORq2 | - | OLq4 | |||
| 1 | 1Rq2 | 1Rq2 | 1Rq2 | - | 1Lq4 | |||
| B | BRq1 | BLq3 | BLq4 | OLqf | BRqf |
 A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −- Q is a finite set of states
- X is the tape alphabet
- B is the blank symbol
- δ is a relation on states and symbols where
δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })kwhere there is k number of tapes - q0 is the initial state
- F is the set of final states
Multi-track Turing machines, a specific type of Multi-tape Turing machine, contain multiple tracks but just one tape head reads and writes on all tracks. Here, a single tape head reads n symbols from n tracks at one step. It accepts recursively enumerable languages like a normal single-track single-tape Turing Machine accepts.
Multi-Track Turing Machine:
A Multi-track Turing machine can be formally described as a 6-tuple (Q, X, ∑, δ, q0, F) where −
- Q is a finite set of states
- X is the tape alphabet
- ∑ is the input alphabet
- δ is a relation on states and symbols where
δ(Qi, [a1, a2, a3,....]) = (Qj, [b1, b2, b3,....], Left_shift or Right_shift) - q0 is the initial state
- F is the set of final states
Non-Deterministic Turing Machine:
In a Non-Deterministic Turing Machine, for every state and symbol, there are a group of actions the TM can have. So, here the transitions are not deterministic. The computation of a non-deterministic Turing Machine is a tree of configurations that can be reached from the start configuration.
An input is accepted if there is at least one node of the tree which is an accept configuration, otherwise it is not accepted. If all branches of the computational tree halt on all inputs, the non-deterministic Turing Machine is called a Decider and if for some input, all branches are rejected, the input is also rejected.
A non-deterministic Turing machine can be formally defined as a 6-tuple (Q, X, ∑, δ, q0, B, F) where −
- Q is a finite set of states
- X is the tape alphabet
- ∑ is the input alphabet
- δ is a transition function;
δ : Q × X → P(Q × X × {Left_shift, Right_shift}). - q0 is the initial state
- B is the blank symbol
- F is the set of final states
A Semi-Infinite Turing Machine:
A Turing Machine with a semi-infinite tape has a left end but no right end. The left end is limited with an end marker.
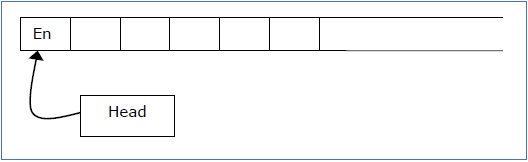 It is a two-track tape −
It is a two-track tape −
- Upper track − It represents the cells to the right of the initial head position.
- Lower track − It represents the cells to the left of the initial head position in reverse order.
The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.
It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.
Note − Turing machines with semi-infinite tape are equivalent to standard Turing machine
Comments
Post a Comment