Normal forms(CNF & GNF)


 CFG:
A CFG is in Chomsky Normal Form if the Productions are in the following forms −
  • A → a
  • A → BC
  • S → ε
where A, B, and C are non-terminals and a is terminal.

Algorithm to Convert into Chomsky Normal Form −

Step 1 − If the start symbol S occurs on some right side, create a new start symbol S’ and a new production S’→ S.
Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)
Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)
Step 4 − Replace each production A → B1…Bn where n > 2 with A → B1C where C → B2 …Bn. Repeat this step for all productions having two or more symbols in the right side.
Step 5 − If the right side of any production is in the form A → aB where a is a terminal and A, B are non-terminal, then the production is replaced by A → XB and X → a. Repeat this step for every production which is in the form A → aB.

Problem

Convert the following CFG into CNF
S → ASA | aB, A → B | S, B → b | ε

Solution

(1) Since S appears in R.H.S, we add a new state S0 and S0→S is added to the production set and it becomes −
S0→S, S→ ASA | aB, A → B | S, B → b | ∈
(2) Now we will remove the null productions −
B → ∈ and A → ∈
After removing B → ε, the production set becomes −
S0→S, S→ ASA | aB | a, A → B | S | ∈, B → b
After removing A → ∈, the production set becomes −
S0→S, S→ ASA | aB | a | AS | SA | S, A → B | S, B → b
(3) Now we will remove the unit productions.
After removing S → S, the production set becomes −
S0→S, S→ ASA | aB | a | AS | SA, A → B | S, B → b
After removing S0→ S, the production set becomes −
S0→ ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA
A → B | S, B → b
After removing A→ B, the production set becomes −
S0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA
A → S | b
B → b
After removing A→ S, the production set becomes −
S0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA
A → b |ASA | aB | a | AS | SA, B → b
(4) Now we will find out more than two variables in the R.H.S
Here, S0→ ASA, S → ASA, A→ ASA violates two Non-terminals in R.H.S.
Hence we will apply step 4 and step 5 to get the following final production set which is in CNF −
S0→ AX | aB | a | AS | SA
S→ AX | aB | a | AS | SA
A → b |AX | aB | a | AS | SA
B → b
X → SA
(5) We have to change the productions S0→ aB, S→ aB, A→ aB
And the final production set becomes −
S0→ AX | YB | a | AS | SA
S→ AX | YB | a | AS | SA
A → b A → b |AX | YB | a | AS | SA
B → b
X → SA
Y → a


GNF:

A CFG is in Greibach Normal Form if the Productions are in the following forms −
A → b
A → bD1…Dn
S → ε
where A, D1,....,Dn are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − If the start symbol S occurs on some right side, create a new start symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)
Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.

Problem

Convert the following CFG into CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o

Solution

Here, S does not appear on the right side of any production and there are no unit or null productions in the production rule set. So, we can skip Step 1 to Step 3.
Step 4
Now after replacing
X in S → XY | Xo | p
with
mX | m
we obtain
S → mXY | mY | mXo | mo | p.
And after replacing
X in Y → Xn | o
with the right side of
X → mX | m
we obtain
Y → mXn | mn | o.
Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p

ii. Ambiguity of Grammars:

If a context free grammar G has more than one derivation tree for some string w ∈ L(G), it is called an ambiguous grammar. There exist multiple right-most or left-most derivations for some string generated from that grammar.

Problem

Check whether the grammar G with production rules −
X → X+X | X*X |X| a
is ambiguous or not.

Solution

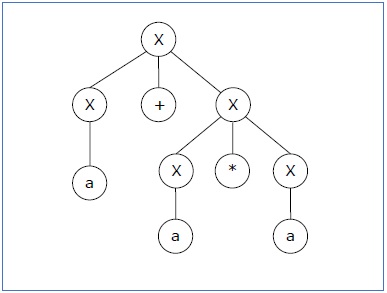
Let’s find out the derivation tree for the string "a+a*a". It has two leftmost derivations.
Derivation 1 − X → X+X → a +X → a+ X*X → a+a*X → a+a*a
Parse tree 1 −
Parse Tree 1 Derivation 2 − X → X*X → X+X*X → a+ X*X → a+a*X → a+a*a
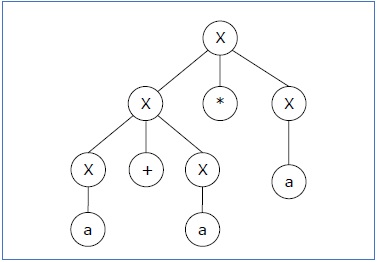Parse tree 2 −
Parse Tree 2 Since there are two parse trees for a single string "a+a*a", the grammar G is ambiguous.

Comments

Post a Comment

Popular posts from this blog

Intelligent Agents(Algorithms for Intelligent Systems)

    Unit II: Intelligent Agents   Intelligent Agents: Agents and Environments, The Concept of Rationality, The Nature of Environments (PEAS), The Structure of Agents: Simple Reflex Agents, Model-Based Reflex Agents, Goal-Based Agents, Utility-Based agents, Learning Agents. Agents and Environments: Agent An  agent  is an entity that perceives its environment through sensors and acts upon that environment through actuators. Agents can be anything from simple programs to complex systems like robots or humans. The key characteristic of an agent is its ability to take actions based on its perceptions to achieve specific goals. Environment The  environment  is the external context or world in which the agent operates. It includes everything the agent can perceive and interact with. The environment provides the agent with inputs (percepts) and receives outputs (actions) from the agent. Example Consider a  self-driving car : ...
Read more

2D-Transformations

Image
Transformation means changing some graphics into something else by applying rules. We can have various types of transformations such as translation, scaling up or down, rotation, shearing, etc. When a transformation takes place on a 2D plane, it is called 2D transformation. Transformations play an important role in computer graphics to reposition the graphics on the screen and change their size or orientation. Homogenous Coordinates To perform a sequence of transformation such as translation followed by rotation and scaling, we need to follow a sequential process − Translate the coordinates, Rotate the translated coordinates, and then Scale the rotated coordinates to complete the composite transformation. To shorten this process, we have to use 3×3 transformation matrix instead of 2×2 transformation matrix. To convert a 2×2 matrix to 3×3 matrix, we have to add an extra dummy coordinate W. In this way, we can represent the point by 3 numbers instead of 2 numbers, wh...
Read more

3D-Transformations(Including projections)

Image
In the 2D system, we use only two coordinates X and Y but in 3D, an extra coordinate Z is added. 3D graphics techniques and their application are fundamental to the entertainment, games, and computer-aided design industries. It is a continuing area of research in scientific visualization. Furthermore, 3D graphics components are now a part of almost every personal computer and, although traditionally intended for graphics-intensive software such as games, they are increasingly being used by other applications. Parallel Projection Parallel projection discards z-coordinate and parallel lines from each vertex on the object are extended until they intersect the view plane. In parallel projection, we specify a direction of projection instead of center of projection. In parallel projection, the distance from the center of projection to project plane is infinite. In this type of projection, we connect the projected vertices by line segments which correspond to connections o...
Read more