Formal Languages and Automata Theory

1. NFA vs DFA

The theory of computation is a branch of computer science that deals with how problems are solved using algorithms. It has three branches, namely; the computational complexity theory, the computability theory, and the automaton theory.

The automaton or automata theory is the study of abstract mathematical machines or systems that can be used to solve computational problems. An automaton is made up of states and transitions, and as it sees a symbol or letter of input, it makes a transition to another state taking the current state and symbol as input.

The automaton or automata theory has several classes that include the Deterministic Finite Automata (DFA) and the Nondeterministic Finite Automata (NFA). These two classes are transition functions of automata or automaton.

In transition, DFA cannot use n empty string, and it can be understood as one machine. If the string ends at a state that is not an acceptable state, DFA will reject it. A DFA machine can be constructed with every input and output.

DFA only has one state transition for every symbol of the alphabet, and there is only one final state for its transition which means that for each character that is read, there is one corresponding state in DFA. It is easier to check membership in DFA but it is more difficult to construct. Backtracking is allowed in DFA, and it requires more space than NFA.

Backtracking is not always allowed in NFA. While it is possible in some cases, in others it is not. It is easier to construct NFA, and it also requires less space, but it is not possible to construct an NFA machine for every input and output.

It is understood as several tiny machines that compute simultaneously, and membership can be harder to check. It uses Empty String Transition, and there are numerous possible next states for each pair of state and input symbol. It starts at a specific state and reads the symbols, and the automaton then determines the next state which depends on the current input and other consequent events. At its accepting state, NFA accepts the string and rejects it otherwise.

Summary:

1.“DFA” stands for “Deterministic Finite Automata” while “NFA” stands for “Nondeterministic Finite Automata.”
2.Both are transition functions of automata. In DFA the next possible state is distinctly set while in NFA each pair of state and input symbol can have many possible next states.
3.NFA can use empty string transition while DFA cannot use empty string transition.
4.NFA is easier to construct while it is more difficult to construct DFA.
5.Backtracking is allowed in DFA while in NFA it may or may not be allowed.
6.DFA requires more space while NFA requires less space.
7.While DFA can be understood as one machine and a DFA machine can be constructed for every input and output, 8.NFA can be understood as several little machines that compute together, and there is no possibility of constructing an NFA machine for every input and output.

 Difference between Mealy and Moore machines

Mealy Machine – A mealy machine is defined as a machine in theory of computation whose output values are determined by both its current state and current inputs. In this machine atmost one transition is possible.
It has 6 tuples: (Q, q0, ∑, O, δ, λ’)
Q is finite set of states
q0 is the initial state
∑ is the input alphabet
O is the output alphabet
δ is transition function which maps Q×∑ → Q
‘λ’ is the output function which maps Q×∑→ O

Diagram –








Moore Machine – A moore machine is defined as a machine in theory of computation whose output values are determined only by its current state.
It has also 6 tuples: (Q, q0, ∑, O, δ, λ)
Q is finite set of states
q0 is the initial state
∑ is the input alphabet
O is the output alphabet
δ is transition function which maps Q×∑ → Q
λ is the output function which maps Q → O
Diagram –



Moore Machine –

1. Output depends only upon present state.
2. If input changes, output does not change.
3. More number of states are required.
4. There is more hardware requirement.
5. They react slower to inputs(One clock cycle later)
6. Synchronous output and state generation.
7. Output is placed on states.
8. Easy to design.

Mealy Machine –

1. Output depends on present state as well as present input.
2. If input changes, output also changes.
3. Less number of states are required.
4. There is less hardware requirement.
5. They react faster to inputs.
6. Asynchronous output generation.
7. Output is placed on transitions.
8. It is difficult to design

 Arden's Theorem:

Statement −

Let P and Q be two regular expressions.

If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*

Proof −

R = Q + (Q + RP)P [After putting the value R = Q + RP]

= Q + QP + RPP

When we put the value of R recursively again and again, we get the following equation −

R = Q + QP + QP² + QP³…..

R = Q (ε + P + P² + P³ + …. )

R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]

Hence, proved.

Assumptions for Applying Arden’s Theorem

• The transition diagram must not have NULL transitions
• It must have only one initial state

Method

Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q₁.

q₁ = q₁R₁₁ + q₂R₂₁ + … + q_nR_n1 + ε

q₂ = q₁R₁₂ + q₂R₂₂ + … + q_nR_n2

…………………………

…………………………

…………………………

…………………………

q_n = q₁R_1n + q₂R_2n + … + q_nR_nn

R_ij represents the set of labels of edges from q_i to q_j, if no such edge exists, then R_ij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of R_ij
Problem
Construct a regular expression corresponding to the automata given below −
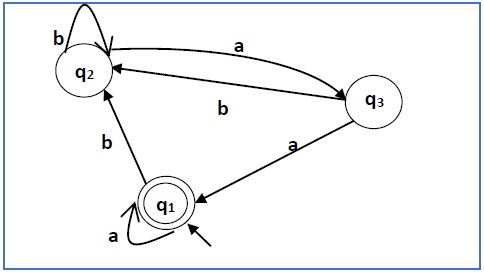Solution −
Here the initial state and final state is q₁.
The equations for the three states q1, q2, and q3 are as follows −

q₁ = q₁a + q₃a + ε (ε move is because q1 is the initial state0

q₂ = q₁b + q₂b + q₃b

q₃ = q₂a

Now, we will solve these three equations −

q₂ = q₁b + q₂b + q₃b

= q₁b + q₂b + (q₂a)b (Substituting value of q₃)

= q₁b + q₂(b + ab)

= q₁b (b + ab)* (Applying Arden’s Theorem)

q₁ = q₁a + q₃a + ε

= q₁a + q₂aa + ε (Substituting value of q₃)

= q₁a + q₁b(b + ab*)aa + ε (Substituting value of q₂)

= q₁(a + b(b + ab)*aa) + ε

= ε (a+ b(b + ab)*aa)*

= (a + b(b + ab)*aa)*

Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −
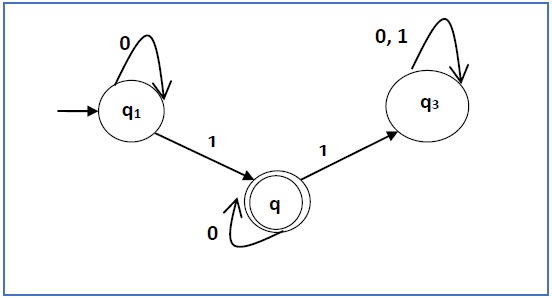Solution −
Here the initial state is q₁ and the final state is q₂
Now we write down the equations −

q₁ = q₁0 + ε

q₂ = q₁1 + q₂0

q₃ = q₂1 + q₃0 + q₃1

Now, we will solve these three equations −

q₁ = ε0* [As, εR = R]

So, q₁ = 0*

q₂ = 0*1 + q₂0

So, q₂ = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.